Add Fractions With Whole Numbers

Addition of Mixed Fractions

We volition acquire how to solve improver of mixed fractions or addition of mixed numbers. There are two methods to add the mixed fractions.

For instance, add 2\(\frac{3}{v}\) and 1\(\frac{three}{10}\).

Nosotros can use the ii methods to add together the mixed numbers.

Method one:

two\(\frac{iii}{5}\) + 1\(\frac{three}{10}\) = (ii + 1) + \(\frac{iii}{5}\) + \(\frac{3}{10}\)  = 3 + \(\frac{three}{5}\) + \(\frac{3}{10}\) = 3 + \(\frac{iii × 2}{5 × 2}\) + \(\frac{3 × one}{10 × 1}\), [L.C.M. of 5 and 10 = 10] = iii + \(\frac{half-dozen}{ten}\) + \(\frac{3}{x}\) = 3 + \(\frac{6 + three}{10}\) = 3 + \(\frac{9}{10}\) = iii\(\frac{9}{10}\)

Step I: We add together the whole numbers, separately. Step II: To add fractions, we have L.C.M. of the denominators and change the fractions into like fractions. Step Three: We find the sum of the whole numbers and the fractions in the simplest form.

Method two:

2\(\frac{3}{5}\) + i\(\frac{iii}{10}\) = (v × ii) + \(\frac{three}{5}\) + (10 × 1) + \(\frac{3}{10}\) = \(\frac{xiii}{5}\) + \(\frac{13}{ten}\) = \(\frac{13 × 2}{five × 2}\) + \(\frac{13 × one}{10 × 1}\), [Fifty.C.G. of 5 and 10 = ten] = \(\frac{26}{10}\) + \(\frac{13}{10}\) = \(\frac{26 + 13}{10}\) = \(\frac{39}{10}\) = three\(\frac{ix}{10}\)

Step I: We change the mixed fractions into improper fractions. Stride II: We have L.C.1000. of the denominators and change the fractions into like fractions. Pace III: We add the like fractions and limited the sum to its simplest form.

At present let united states consider some of the examples on improver of mixed numbers using Method 1.

1. Add ane\(\frac{1}{half-dozen}\) , 2\(\frac{1}{8}\)and 3\(\frac{one}{4}\)

Solution:

1\(\frac{1}{six}\) + 2\(\frac{i}{8}\) + 3\(\frac{1}{iv}\)

Allow united states add whole numbers and fraction parts separately.

= (ane + 2 + 3) + (\(\frac{1}{half-dozen}\) + \(\frac{1}{8}\) + \(\frac{ane}{4}\))

= 6 + (\(\frac{one}{6}\) + \(\frac{1}{viii}\) + \(\frac{one}{4}\))

= 6 + \(\frac{1 × 4}{6 × iv}\) + \(\frac{ane × iii}{viii × 3}\) + \(\frac{1 × 6}{four × 6}\); [Since, the L.C.M. of six, 8 and four = 24]

= half-dozen + \(\frac{4}{24}\) + \(\frac{3}{24}\) + \(\frac{6}{24}\)

= half-dozen + \(\frac{4 + iii + six}{24}\)

= 6 + \(\frac{13}{24}\)

= 6\(\frac{13}{24}\)

2. Add5\(\frac{1}{ix}\), 2\(\frac{1}{12}\) and \(\frac{3}{iv}\).

Solution:

five\(\frac{one}{nine}\) + 2\(\frac{1}{12}\) + \(\frac{iii}{4}\)

Allow the states add whole numbers and fraction parts separately.

= (5 + 2 + 0) + (\(\frac{one}{9}\) + \(\frac{1}{12}\) + \(\frac{three}{4}\))

= 7 + \(\frac{1}{9}\) + \(\frac{ane}{12}\) + \(\frac{3}{iv}\)

= 7 + \(\frac{1 × 4}{ix × iv}\) + \(\frac{1 × 3}{12 × 3}\) + \(\frac{3 × 9}{4 × 9}\), [Since the L.C.M. of nine, 12 and 4 = 36]

= vii + \(\frac{iv}{36}\) + \(\frac{3}{36}\) + \(\frac{27}{36}\)

= vii + \(\frac{iv + 3 + 27}{36}\)

= 7 + \(\frac{34}{36}\)

= 7 + \(\frac{17}{xviii}\),

= 7\(\frac{17}{18}\).

3. Add \(\frac{5}{6}\), 2\(\frac{one}{2}\) and three\(\frac{one}{4}\)

Solution:

\(\frac{five}{6}\) + 2\(\frac{1}{two}\) + 3\(\frac{1}{4}\)

Permit usa add whole numbers and fraction parts separately.

= (0 + 2 + three) + \(\frac{5}{6}\) + \(\frac{one}{ii}\) + \(\frac{ane}{4}\)

= 5 + \(\frac{5}{6}\) + \(\frac{1}{2}\) + \(\frac{1}{4}\)

= 5 + \(\frac{v × 2}{half-dozen × 2}\) + \(\frac{1 × 6}{two × 6}\) + \(\frac{ane × three}{4 × three}\), [Since, the Fifty.C.K. of half-dozen, 2 and four = 12]

= 5 + \(\frac{10}{12}\) + \(\frac{half-dozen}{12}\) + \(\frac{3}{12}\)

= five + \(\frac{10 + 6 + 3}{12}\)

= v + \(\frac{xix}{12}\); [Here, fraction \(\frac{19}{12}\) can write equally mixed number.]

= 5 + 1\(\frac{7}{12}\)

= v + 1 + \(\frac{7}{12}\)

= 6\(\frac{vii}{12}\)

4. Add 3\(\frac{5}{viii}\)and 2\(\frac{2}{iii}\) .

Solution:

Let usa add whole numbers and fraction parts separately.

iii\(\frac{5}{8}\) + two\(\frac{2}{3}\)

= (3 + 2) + ( \(\frac{v}{eight}\) + \(\frac{two}{three}\))

= 5 + ( \(\frac{v}{8}\) + \(\frac{2}{iii}\))

Fifty.C.M. of denominator viii and 3 = 24.

= 5 + \(\frac{5 × 3}{8 × 3}\) + \(\frac{2 × 8}{3 × 8}\), (Since, L.C.M. of 8 and 3 = 24)

= v + \(\frac{15}{24}\) + \(\frac{sixteen}{24}\)

= five + \(\frac{15 + xvi}{24}\)

= 5 + \(\frac{31}{24}\)

= 5 + 1\(\frac{7}{24}\).

= 6 \(\frac{7}{24}\).

Now allow us consider some of the examples on add-on of mixed numbers using Method 2.

ane.Add 2\(\frac{3}{9}\), 1\(\frac{1}{6}\)and ii\(\frac{two}{3}\)

Solution:

2\(\frac{3}{9}\) + one\(\frac{1}{vi}\) + 2\(\frac{2}{3}\)

= \(\frac{(9 × 2) + three}{ix}\) + \(\frac{(6 × 1) + 1}{6}\) + \(\frac{(3 × 2) + two}{3}\)

= \(\frac{21}{9}\) + \(\frac{vii}{half-dozen}\) + \(\frac{8}{3}\), (50.C.K. of ix, half dozen and 3 = 18)

= \(\frac{21 × 2}{nine × 2}\) + \(\frac{7 × three}{half-dozen × three}\) + \(\frac{8 × 6}{three × 6}\)

= \(\frac{42}{eighteen}\) + \(\frac{21}{18}\) + \(\frac{48}{18}\)

= \(\frac{42 + 21 + 48}{xviii}\)

= \(\frac{111}{xviii}\)

= \(\frac{37}{vi}\)

= 6\(\frac{one}{6}\)

2. Add together2\(\frac{ane}{two}\), 3\(\frac{1}{three}\) and iv\(\frac{one}{4}\).

Solution:

2\(\frac{1}{2}\) + 3\(\frac{1}{3}\) + iv\(\frac{1}{4}\)

= \(\frac{(2 × two) + 1}{2}\) + \(\frac{(iii × iii) + one}{three}\) + \(\frac{(4 × 4) + 1}{3}\)

= \(\frac{5}{2}\) + \(\frac{ten}{3}\) + \(\frac{17}{four}\), (50.C.M. of 2, iii and 4 = 12)

= \(\frac{5 × vi}{two × 6}\) + \(\frac{10 × 4}{3 × four}\) + \(\frac{17 × 3}{4 × 3}\), (Since, L.C.Yard. of 2, iii and four = 12)

= \(\frac{30}{12}\) + \(\frac{40}{12}\) + \(\frac{51}{12}\)

= \(\frac{30 + forty + 51}{12}\)

= \(\frac{121}{12}\)

= x\(\frac{one}{12}\)

3. Add 3\(\frac{5}{viii}\) and 2\(\frac{two}{iii}\) .

Solution:

3\(\frac{v}{8}\) + 2\(\frac{2}{three}\)

Let u.s. convert the mixed fractions into improper fractions.

= \(\frac{(8 × 3) + 5}{8}\) + \(\frac{(three × 2) + ii}{3}\)

= \(\frac{29}{viii}\) + \(\frac{viii}{iii}\),

50.C.M. of denominator 8 and three = 24.

= \(\frac{29 × three}{8 × 3}\) + \(\frac{eight × 8}{iii × viii}\), (Since, L.C.K. of 8 and 3 = 24)

= \(\frac{87}{24}\) + \(\frac{64}{24}\)

= \(\frac{87 + 64}{24}\)

= \(\frac{151}{24}\)

= 6\(\frac{7}{24}\).

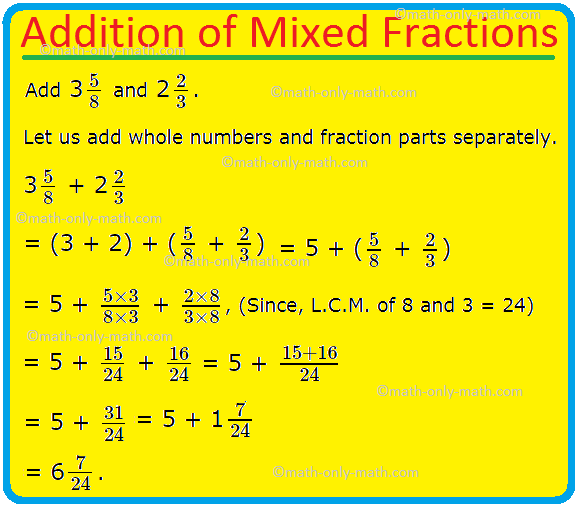
Word Problem on Addition of Mixed Fraction:

The doctor advises every child to beverage 3\(\frac{one}{two}\) litres of water in morning, 4\(\frac{1}{iv}\) litres in the afterward noon and \(\frac{1}{2}\) litre earlier going to bed. How much h2o should a child drink every day?

Solution:

3\(\frac{1}{2}\) + 4\(\frac{1}{4}\) + \(\frac{1}{2}\)

Let us add whole numbers and fraction parts separately.

= (3 + 4 + 0) + ( \(\frac{ane}{2}\) + \(\frac{1}{4}\) + \(\frac{1}{two}\))

= 7 + ( \(\frac{one}{2}\) + \(\frac{one}{4}\) + \(\frac{one}{two}\) )

L.C.M. of denominators 2, 4 and 2 = iv.

= vii + \(\frac{1 × 2}{ii × 2}\) + \(\frac{i × 1}{4 × 1}\) + \(\frac{1 × 2}{2 × 2}\), [Since, the L.C.Grand. of 2, 4 and 2 = 4.]

= 7 + \(\frac{2}{4}\) + \(\frac{1}{four}\) + \(\frac{2}{4}\)

= 7 + \(\frac{2 + 1 + 2}{4}\)

= seven + \(\frac{v}{iv}\)

[Here, the fraction \(\frac{5}{iv}\) tin can write every bit mixed number.]

= 7 + 1\(\frac{1}{4}\)

= eight\(\frac{1}{4}\)

Therefore,viii\(\frac{1}{4}\) litres of water should a child beverage every twenty-four hours.

●Related Concepts

• Fraction of a Whole Numbers
• Representation of a Fraction
• Equivalent Fractions
• Properties of Equivalent Fractions
• Finding Equivalent Fractions
• Reducing the Equivalent Fractions
• Verification of Equivalent Fractions
• Finding a Fraction of a Whole Number
• Similar and Unlike Fractions
• Comparison of Like Fractions
• Comparison of Fractions having the same Numerator
• Comparison of Different Fractions
• Fractions in Ascending Gild
• Fractions in Descending Social club
• Types of Fractions
• Irresolute Fractions
• Conversion of Fractions into Fractions having Same Denominator
• Conversion of a Fraction into its Smallest and Simplest Course
• Add-on of Fractions having the Same Denominator
• Addition of Dissimilar Fractions
• Addition of Mixed Fractions
• Word Problems on Addition of Mixed Fractions
• Worksheet on Discussion Problems on Addition of Mixed Fractions
• Subtraction of Fractions having the Same Denominator
• Subtraction of Unlike Fractions
• Subtraction of Mixed Fractions
• Give-and-take Problems on Subtraction of Mixed Fractions
• Worksheet on Word Problems on subtraction of Mixed Fractions
• Add-on and Subtraction of Fractions on the Fraction Number Line
• Word Problems on Multiplication of Mixed Fractions
• Worksheet on Word Problems on Multiplication of Mixed Fractions
• Multiplying Fractions
• Dividing Fractions
• Give-and-take Issues on Sectionalisation of Mixed Fractions
• Worksheet on Discussion Problems on Sectionalisation of Mixed Fractions

Didn't find what you were looking for? Or want to know more data about Math Only Math. Use this Google Search to discover what you need.

Add Fractions With Whole Numbers,

Source: https://www.math-only-math.com/addition-of-mixed-fractions.html

Posted by: rileywithery.blogspot.com

Share this post